SNES Assembly Adventure 06: More On Subroutines

Update February 2022: All code examples from all articles in this series can now be found on Github in one repository

Welcome back, Adventurer. The last time, we looked at subroutines and how they work. We will look a bit deeper into the stack and subroutines. So in this article, we will

• Learn about different ways to pass arguments to subroutines
• Write code to calculate the total stopping time of the Collatz Conjecture

There will be little to no SNES-specific content here. This is more about building on the knowledge from the article on subroutines. But these new techniques will help us improve the sprite demo from part 4.

Enough talk, let’s get started!

Passing Arguments to Subroutines

When we use a function in a high-level programming language like C, we often pass arguments to the function. Arguments or parameters are passed to the function and it uses these to perform operations. After all, operations are done, the function (potentially) returns a result to the caller, and code execution resumes after the function call.

Mind that the terms argument and parameter are often used interchangeably; it’s not 100% correct depending on which language you’re talking about, but for our purposes, it is sufficient to say arguments and parameters are the same things.

Now, how are we going to pass arguments to a subroutine? There are two basic possibilities. In the article on subroutines, we wrote a simple subroutine called AddXtoY. Here’s the code as a reminder:

Focus on lines 13 and 14. Before we call the subroutine, we load the two values we want to add into the X and Y registers. This is called Pass-by-Register. We pass the values we want the subroutine to use by loading them into a certain register or registers. While this is convenient and easy to do, it has several disadvantages. For one, it limits the number of arguments we can pass to the number of registers we have at our disposal. In the case of the 65816, that means no more than three 16-bit arguments (A, X, and Y registers). That’s not a lot. Besides that, it also destroys the current values stored in those registers. So if you wish to use some of the values currently in one of the registers after the subroutine, you’d need to store them somewhere else first. Then you’d load the arguments into the registers, call the subroutines, then load the old values back into the registers. Not very efficient.

And what about returning values? In the scenario above, you’d need to store the return values in the same (up to) three registers you passed the arguments with. But what if you want to use the values the registers held before the subroutine call? You’d need to store the return value(s) somewhere and…

You get the point. Pass-by-Register can be effective if you’re working with only little to no arguments. But there is a myriad of disadvantages. So while this might be sufficient for simple subroutines, if you’re going to write more complex games, you’ll need more complex subroutines. Passing arguments by register will only give you limited options. You’ll need to do a lot of copying data from registers to memory and back again. Not very effective and error-prone.

Another way would be to reserve a certain range of memory to store arguments and return values. While this lets us reduce the number of data transfers between memory and registers, it still comes with some problems. One, it is somewhat inflexible, since it is hard to know how many arguments and/or return values a subroutine will need. You’d need to reserve an arbitrary number of memory locations for subroutine arguments and return values. This is a waste of memory. The next problem is access by other parts of the program. If another part of the program overrides the reserved memory locations with other data, your subroutine will work with the wrong data.

So reserving certain memory locations for storing arguments and return values is also suboptimal.

Now, if only there was a way to store and retrieve data in memory without the need to keep track of the addresses…

Passing Arguments by Stack

This is the technique I prefer to use in most of my code. It is a bit more complicated to understand (but not to implement). But it offers the most flexibility and will improve overall code quality. Another nice side-effect of this is that your code will be re-entrant. This is fancy computer science talk for the subroutine can be interrupted (by an interrupt) and resume execution after returning from the interrupt handler/routine without problems.

This is the general idea of passing arguments by stack:

• Before calling the subroutine, push all arguments that the subroutine needs to the stack
• Call the subroutine
• In the subroutine, pull the arguments from the stack and use them
• Return from the subroutine to the caller (a program or other subroutine that calls a subroutine is the caller while the called subroutine is the callee)
• Continue execution where the caller left off

Let’s see this in action with a simple example.

Collatz Conjecture

We will write a subroutine that will be calculated the stopping time for the Collatz Conjecture. A conjecture is a mathematical hypothesis that has yet to be proven. Here’s the function definition:

That’s simply fancy math talk for, “if n is even, divide it by two; else, multiply it by three and add one.”

The Collatz Conjecture says that for any positive integer this algorithm will always yield a result of one after a finite number of steps. We want to calculate the number of steps it takes until n equals one, a.k.a., the total stopping time.

Here’s the code. Read it carefully but don’t be thrown off, there is a new addressing mode (and we love new addressing modes), and looks like absolute addressing. But it is something new. More after the code:

I won’t go through the code linearly, but rather follow it logically. So don’t be thrown off when I jump lines. All code will be explained. Let’s dive right into this!

Lines 3 through 11: There should be no surprises here. We switch to native mode, set the index registers to 16-bit, the accumulator to 8-bit, and set the stack pointer to $1fff. Standard setup.

Lines 14 through 17: This code shouldn’t be hard to figure out, too. You already know how the stack works. First, we load the integer whose total stopping time we want to calculate into A and push it to the stack. Then, we push a second zero-byte to the stack. This is a placeholder and will, after the subroutine returns, hold the result.

I’ll introduce this graphic here to keep track of the stack. Here’s how the stack looks after we pushed two bytes to it:

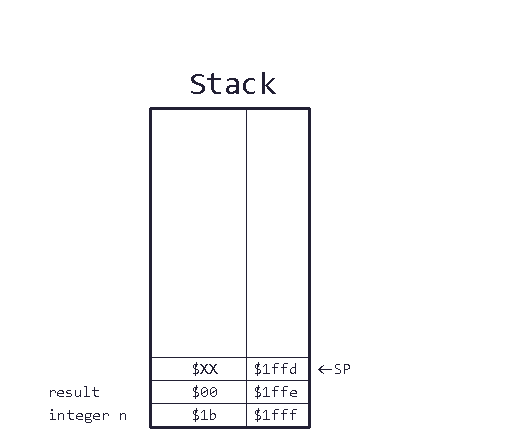
Line 18: We call the subroutine! So jump ahead to line 29.

Lines 29 through 32: Boy, three new instructions. Let’s check them out:

phd : PusH Direct register
tsc : Transfer Stack pointer to C accumulator
tcd : Transfer C accumulator to Direct register

Mind that tsc and tcd will always transfer 16-bit numbers regardless of whether the memory/accumulator select flag is set or not.

What we are doing in these three lines of code, is to create a so-called frame pointer. In very simple terms, frame pointers are a technique that allows us to create local variables within our subroutine that won’t clutter or overwrite existing memory locations. In our case, we will use this frame pointer to access the two bytes we pushed to stack before with a new addressing mode. Our frame pointer will be stored in the Direct Register.

We create our frame pointer by first pushing the current content of the direct register to the stack (we’ll shortly see why). Then, we transfer the current stack pointer content to the direct register (we can’t transfer data directly from the direct register to stack pointer, so we take a detour through the accumulator). Let’s look at the stack now:

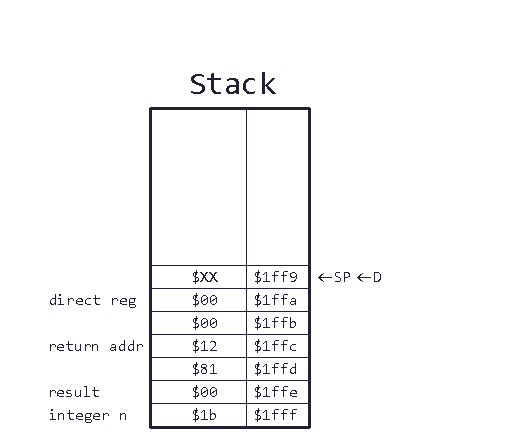
I added a second arrow that represents the current value of the direct register. There are four new bytes on the stack. The return address jsr pushed to the stack as we discussed last time, and the content of the direct register (remember that on startup/reset the direct register is set to zero automatically).

Lines 34 and 35: Here we define two local constants. Mind, that this will not assemble into actual code. The assembler will simply replace all instances of StepCount with $05, and Input with $06. This will make sense in a second.

Line 37: Here’s where the new addressing mode comes into play. What we do here is called direct addressing. How does it work? Here’s a graphic:

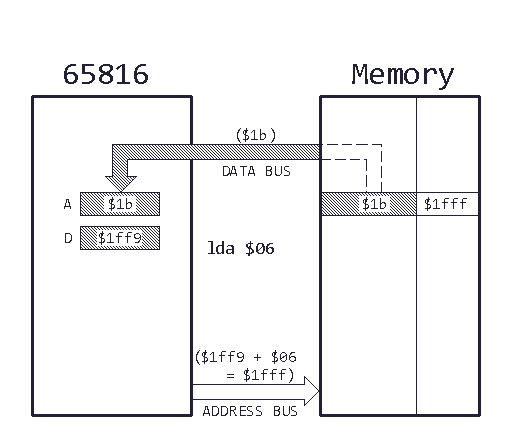
Direct addressing works like this: The CPU takes the current value from the direct register and adds the operand supplied by the opcode. Let’s look at the stack again:

We can see, that our input value $1b is six bytes beyond the direct register, the result byte five. Last time we learned about stack relative addressing. Direct addressing works in a very similar way with a slightly different syntax only.

We could access the two bytes also with lda $05, S and lda $06, S respectively. Why do we go through the extra trouble of setting up a frame pointer for this?

The answer is pretty simple: If we were to use stack relative addressing to access the two bytes, we couldn’t use the stack in this subroutine. As soon as we’d push or pull from the stack, the stack pointer would change, and lda $05, S would point to another address than before. Using the direct register instead will let us use the stack in this subroutine to our heart’s content. And we will make use of the stack again shortly.

(Remember that we’re working with an accumulator that is 16-bit now. The 65816 is a little endian machine, so the CPU will load the byte from the effective address into the low-byte, the byte at effective address + 1 into the high-byte of the accumulator.)

Lines 37 through 40: Before we start calculating the total stopping time, we will create a local 16-bit variable to store the intermediate results. We need a 16-bit number to hold the intermediate results because an 8-bit number could only hold numbers up to 255. If you look at the calculation example on the Wikipedia page I linked, you can see that calculating the total stopping time may result in intermediate results way larger than 255. This way, we can hold results of up to 65535.

To this end, we first load our start value with lda Input (same as lda $06), so now the accumulator holds $1b. Next, we set the accumulator to 16-bit. We use a bit-wise AND operation to clear the upper byte of the accumulator. Now we push the new 16-bit number onto the stack:

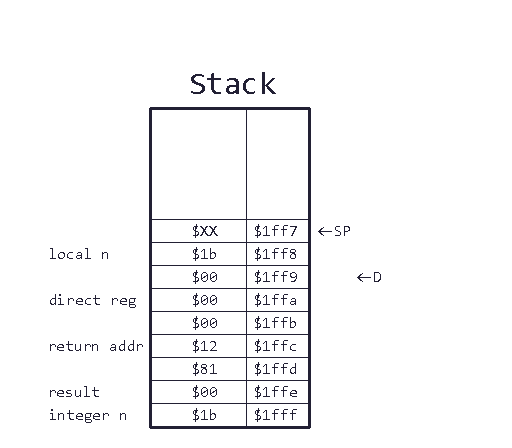
See how the stack pointer has moved? We could no longer use lda $06, S to access our input value. But the direct register lets us still access data without a problem.

Now that all is set up, time to actually calculate the total stopping time.

Lines 42 through 45: Here we check if n has already reached one. We load the current value of n and decrement it. If after decrementing the accumulator holds zero, n is obviously one, so we branch to the end of the subroutine (marked with the label Return) to return to the caller (if you wonder why I don’t simply do a cmp #$01 check, remember that cmp will check whether the accumulator value is equal or greater than the operand. So this would always check and the subroutine would always branch to Return).

Lines 47 through 55: Checking whether a number is odd or even is really simple with binary numbers. If the least significant bit is set, then it is an odd number, otherwise, it is an even number. This check is pretty simple: We load $0001 into the accumulator and do a bit-wise AND operation against the current value of n. If n is odd (so the result of and is $0001), we skip the code and branch to the label CheckOdd.

If n is even, we need to divide n by two as stated in the Collatz Conjecture function above. Dividing by two is again pretty simple with binary numbers. We just need to shift the bits one bit to the right. So we first pull n from the stack with pla into the accumulator, shift it one bit to the right with lsr (Logic Shift Right), and push it back to stack with pha.

“Why not simply do lsr $01, S?”, you might ask. Here comes a limitation into play I mentioned back in article 2. The 65816 does not have an orthogonal instruction set. This means not every opcode can use every addressing mode. Unfortunately, lsr does not support stack relative addressing. So we must take the extra step to first load the current value of n into the accumulator (if you’re wondering why I use pla/pha when lda/sta would work too, this is a small code optimization: lda, sta, and pla will all take five cycles each, but pha will only take four; so I save one cycle on each iteration).

Once that is done, line 54 uses direct addressing to increment the step counter by one. After we have done that, we jump back to CheckOne to see if n has already reached one.

Let’s see now what happens when the branch check in line 50 passes and n is actually odd.

Lines 57 through 63: As of the function above, when n is odd, we need to multiply n by three and add one.

I decided to extract the code for multiplying n by three into a separate subroutine. This is not the most efficient way to do this, but my goal here is to demonstrate how to pass arguments by stack. And that this will even work when calling subroutines within subroutines.

Here’s the current stack again:

The argument is already on the stack so we can call the subroutine MulByThree directly.

Lines 76 through 80: Within the MulByThree subroutine, we first do exactly what we did in Collatz. We save the caller’s frame pointer and “create” a new one for this subroutine. Let’s look at the stack once more:

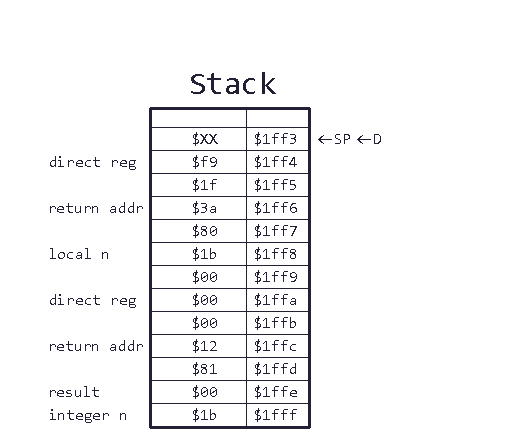
as you can see, the stack has grown. It now additionally holds the return address to Collatz and the frame pointer of Collatz.

Line 82: Since we updated the direct register with a new value, we can again use the same technique as above to access arguments stored on the stack with direct addressing.

Lines 83 through 88: This should be obvious. We load the current value with direct addressing from stack, multiply the current value by three by adding it to itself twice and store it back on stack.

Lines 89 and 90: After we multiplied by three and stored the result back on stack, we pull the caller’s frame pointer back into the direct register and finally return to the caller.

Now we jump back to subroutine Collatz.

Lines 59 through 63: After multiplying by three, we need to add one to the new value. So we pull it from stack, increment, back to stack. Increment the step counter too, then branch to CheckEven. Why not to CheckOne? Because if you look at the formula 3n+1 it is easy to see that there is no positive n where 3n + 1=1 is true. It wouldn’t hurt to branch to CheckOne since the test would simply fail every time; you’d just be wasting precious cycles.

Lines 65 through 69: Once n reaches one, the subroutine will jump here. Let’s look at the stack again quickly:

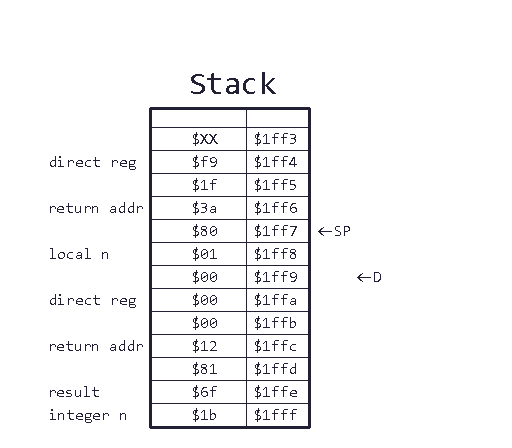
This code does a little clean-up before returning to the caller. First, we pull n from stack to make sure the stack pointer points to the caller’s frame pointer/direct register content. Then we set the accumulator back to 8-bit. Finally, we pull the caller’s frame pointer and return to the caller.

Lines 19 through 21: Now back from the Collatz subroutine we can simply pull the result from the stack. Remember to pull the original n from stack, too. Always clean up after yourself on the stack! Finally, we loop forever.

There are a few things to keep in mind about this code. One, this is not the fastest or most efficient way to calculate the total stopping time. There are a lot of things I did for the sake of demonstrating certain concepts (or limitations). For example, the lines 51 through 53 would be replaced with an lsr instruction that uses direct addressing (can you find the correct offset you need to give it? Use the stack graphic!). But I wanted to show you how certain opcodes won’t let you use an addressing mode and how to work around that. I also described above how the MulByThree subroutine could be completely incorporated into the Collatz subroutine.

For reference, here is the complete code with some additional code to make it run in bsnes+. Check the instructions in part 4 on how to build code for the SNES:

And this is how you pass arguments by stack to subroutines. It may seem convoluted and overblown now. But when we improve the sprite demo from part 4 with subroutines, the advantages will become apparent. Further down the line, I’ll show you how to further improve your code with subroutine launchers. Here passing arguments by stack is the safe way to pass arguments.

Conclusion

Wow, that was a lot of text! This was a bit heavy on the theory side of things. But I think it will help you a lot down the line to write working code and keep things manageable. Next time, we’ll use subroutines to improve the sprite demo from part 4 and make the sprites bounce off the screen boundaries.

Links and Reference

• A Wiki page detailing different techniques of passing arguments to subroutines. Some of the things discussed here are described there.
• This page explains the different stack opcodes in more detail.
• All SNES Assembly Adventure code examples of this series on Github